Notoj de Biblioteko Sakura
Ni publikigas jenajn partojn el la originalo:
"Antaŭparolo de D-ro Ooiŝi", "Parto I. Sciencaj Artikoloj".
Minimuma revizio estas farita:
(1) La vortoj piednotitaj de la originala redaktinto estas renumerite markitaj per (n).
(2) Mistajpoj kaj kelkaj simplaj eraroj estas korektitaj, kiujn ni listigis en la tabelo de reviziitaj vortoj. La listigitaj vortoj estas numeritaj kun asterisko *n.
(3) Dubindaj kazoj kaj senkomentaj mallongigoj estas lasitaj.
Averto
Ĉi tiu teksto enhavas esprimojn, kiuj povas esti ne konformaj al la nuna ĝenerala kriterio de internaciaj amikaj rilatoj. Ni senmodife publikigas ilin, kiel skribite en la originalo.
Historia fono: Japanujo aneksis Koreujon en 1910, kaj daŭris tiel ĝis 1945.
D–ro Nakamura naskiĝis en Hagi, Jamaguĉi Gubernio, la 19-an de Aprilo 1855. Li studis fizikon en Imperia Universitato en Tokio. En 1890 li fariĝis inĝeniero de Japana Centra Meteorologia Observatorio*1 kaj poste ĝia direktoro en 1895. Li ricevis la titolon de doktoro de scienco en 1902, kaj de 1908 li estis membro de Japana Imperia Akademio.
Li kiel sciencisto estis fame konata ne nur en Japanujo, sed ankaŭ tra la tuta mondo. Kvar fojojn li vizitis Eŭropon por studi sciencon aŭ ĉeesti sciencistajn konferencojn.
Por la unua fojo li ekkonis nian lingvon en 1907, kiam li veturis al Francujo per franca ŝipo, sur kiu li konatiĝis kun oficisto de Hidrografia Departemento de la celita lando. Tiu fremda sinjoro parolis al li pri Esperanto, kaj de tiu okazo li komencis lerni la lingvon.
En Julio 1909 li aliĝis al la tiama centra institucio de la japana esperantistaro, Japana Esperantista Asocio, kaj de tiam li ĉeestadis preskaŭ ĉiam en esperantistaj kunsidoj. En 1914 oni elektis lin kiel vicprezidanton de la asocio. (Tiam la prezidanto de l' asocio, Grafo Tadasu Hajaŝi, Ministro por Enlandaj Aferoj, jam estis mortinta kaj vakis la seĝo de prezidanto kaj tial li estis en la fakto la ĉefa gvidanto de la asocio). En la daŭro de la jaroj de 1910 ĝis 1915, nia movado estis tre malvigla kaj la asocio ne povis aperigi sian organan gazeton regule. Dum tiaj malfacilaj tempoj li subtenadis nian aferon ne nur morale sed ankaŭ materiale. La III-an Kongreson de Japanaj Esperantistoj, kiun oni havis en 1915 en Tokio, li prezidis kiel la ĉefo de la asocio, kaj de tiam li ĉiam ĉeestis la kongresojn kaj ilin gvidis.
Post la dissolviĝo de l' asocio (1919), fondiĝis Japana Esperanto-Instituto kaj li fariĝis konsilanto de la nova centro de la japana Esperanto-movado. Kiam ĝi ŝanĝis sian statuton en 1926 kaj estis leĝe personigita kun la permeso de la registaro, li fariĝis ĝia ĉefdirektoro.
Ni memoras tre bone, kiel li aperis en nia kunsido kun tiuj neforgeseblaj blanka hararo kaj milda vizaĝo kaj ĝojigis ĉeestantojn. Li restis sur la seĝo ĝis kiam li finis la surteran vivon de 75 jaroj la 3-an de Januaro 1930. Kaj kvankam jam ni ne povas plu vidi lin inter niaj vicoj, ni povas ankoraŭ aŭdi la eĥon de lia bonhumora rideto kaj bonkorajn afablajn vortojn, kiujn li ofte eldiris al ni, laborantoj por Esperanto.
Ni respektis kaj amis lin kiel patron. Kaj lia nobla karaktero postvivas lin en nia memoro, kaj ĉiam instigas nin al fervora laborado por la sankta afero.
Li uzis nian lingvon ne nur en Esperantujo, sed ankaŭ en sia specialo. Li verkis ne malmultajn artikolojn sciencajn por fakaj revuoj. Kaj krom tio, li ankaŭ tradukis juvelajn pecojn el klasika ĥina kaj japana literaturoj, el kiuj plejparto jam aperis en "La Revuo Orienta", oficiala organo de Japana Esperanto-Instituto.
Jen ni kompilis ilin kune kun la restantaj ankoraŭ ne publikitaj verkoj en unu volumon, kaj prezentas ĝin al la tutmonda esperantistaro.
Tokio, en Aprilo 1932.
La mezurado de la intenseco de la falanta pluvo estas tre utila ne sole de la praktika vidpunkto, sed ankaŭ de la teoria; sed ĝis nun oni efektivigis nur tre malofte tian mezuradon, ĉar ĝi ĉiam multe kostas al ni tempon kaj laboron.
En nunaj tempoj, kiam oni jam posedas diversajn bonajn pluvografojn, oni povas facile kalkuli la pluvintensecon per tanĝantoj strekitaj ĉe ĉiu punkto de la pluvografa kurbo. Tiu ĉi procedo tamen estas nur bona por pluvo ne tre forta, sed ĝi tute ne taŭgas, kiam la pluvo estas tre forta kaj sekve la kurbo tre kruta, ĉar en tiu okazo oni povas havi diversajn valorojn de la intenseco tre diferencajn unuj de la aliaj laŭ la maniero, ke oni strekas tanĝanton iom pli aŭ malpli tro krutan. En la lasta oktobra kajero de la Quarterly Journal of the Royal Meteorological Society publikigis sinjoro R. Corless sian tre interesan verkon pri la pluvintenseco ĉe Kew. Li aplikis al la kurboj de Beckley'a pluvografo la tanĝantmetodon, uzante la diferentiatoron elpensitan de Dr. J. Erkine Murray. Malfeliĉe mi ne ankoraŭ konas tiun instrumenton kaj tial mi ne povas juĝi, ke ĝi trudas al ni kiom da tempo kaj laboro. Cetere sinjoro Corless ankaŭ konfesas, ke oni ne povas eviti la supre diritan malutilon eĉ per tiu instrumento.
La registrilo de pluvintenseco uzata en la japana centra meteorologia observejo donas tre belan kurbon, kiu sufiĉe fidele prezentas la pluvintensecon. Pri tiu ĉi instrumento sinjoro Dr. Oiŝi priskribis jam en la lasta maja kajero de tiu ĉi ĵurnalo, sed ĉar li skribis japane, la plej multo da alilandaj legantoj ne povus ĝin kompreni. Tial mi volas reskribi pli detale pri ĝi, por ke oni povu juĝi ĝian taŭgecon.
La ilo konsistas el U-forma tubo, kies unu branĉo estas multe pli longa ol la alia; en ĝia malsupra parto sin trovas hidrargo, sur kies supraĵo en la pli mallonga branĉo naĝas flosaĵo F, kiu povas movi supren malsupren*2 laŭ la niveloŝanĝo de la hidrargo; sur la pli longa branĉo estas lutita*3 unu perpendikla je ĝi kapilartubo K, kiu kuŝas iom pli alte ol la flosaĵo. La longo de la kapilartubo estas tiel elektita, ke, kiam oni metas akvon en la pli longan tubon, ĝi elfluu el la kapilartubo kun rapido proporcia je la alteco NK de la akvo troviĝanta super la truo, el kiu ĝi defalas.
Kiam oni uzas hidrargon, la amplekso de movo de la flosaĵo estas tre malgrandigata, kaj tial oni estas devigita provizi la vekton OCP, por ke la plumo P povu movi pli amplekse kaj montri ĉiujn ŝanĝojn de pluvintenseco eĉ tre malgrandajn. Sekve la uzado de hidrargo estas plivole eviti, sed ĝi tamen estas nepre necesa, ĉar alie la kapilara forto altirante flanken la flosaĵon tute malhelpas ĝian movon.
Cetere, tia vekto havas tian malutilon, ke la plumo strekas cirklan arkon, kiam ĝi devas streki rekton. Por eviti tiun malutilon mi elektis la vektosistemon montritan en la figuro II. La vekto OD turniĝas ĉirkaŭ la horizontala akso fiksita en O; la vekto PB, kies longo estas duobla kiel OD, estas artikita en sia mezo D kun la vekto OD; ĉe unu el siaj ekstremoj ĝi portas plumon P, dum ĉe la alia ĝi glitas libere sur horizontala rekto OK kuŝanta sur la sama nivelo kiel la akso O. Tiamaniere la punkto P ĉiam restas sur la vertikalo strekita je O.
Estu nun y la profundeco de akvo super la kapilara tubo, S la areo de la U-tubo*4, m la pluvintenseco, supozite konstanta*5, t. e. la pluvokvanto eniranta en la tubon dum ĉiu unuo de tempo, kaj fine k la intenseco de akvo elfluanta el la kapilara tubo, kiam la profundo de l' akvo estas unuo de longo. Tiam oni povas skribi jenan ekvacion:
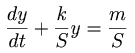
kaj de tio sekvas
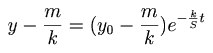
En nia instrumento la kvanto da akvo, kiu elfluas ĉiu minute el la kapilara tubo, estas 75 gramoj, kiam y estas 30 centimetroj, oni do havas k=2.5; cetere S=0.5 kvadratcentimetro, sekve ![]() . Oni nun povas de tio konkludi, ke tuj post duono da minuto la eraro fariĝas jam pli malgranda ol 13%.
. Oni nun povas de tio konkludi, ke tuj post duono da minuto la eraro fariĝas jam pli malgranda ol 13%.
Por vidi, kian eraron oni devas havi, kiam la pluvintenseco ŝanĝiĝas periode, mi faris ankaŭ jenan kalkulon. Mi supozis, ke la pluvintenseco estu prezentita per ![]() ; en tia okazo oni trovas
; en tia okazo oni trovas
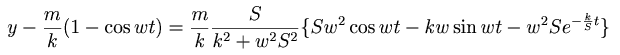
kaj plie se oni supozas, ke la periodo estu 12 minutoj, oni havas por nia instrumento
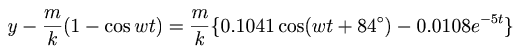 .
.
Oni povas klare vidi per ĉi tio, ke la eraroj estas ĉiam tre malgrandaj, ke la amplekso estas neniom ŝanĝita kaj ke nur la fazo malfruas ĉirkaŭ 1/5 de minuto. Cetere tiu ĉi konkludo estis plene certigita per nia eksperimento.
La faktoro k estas iom ŝanĝebla laŭ la temperaturo kaj la stato de la kapilara tubo, tre pura aŭ ne; sed oni ĉiam povas determini ĝin per tre facila eksperimento.
Por montri la taŭgecon de nia instrumento, mi aldonas tie ĉi kelke da kurboj strekitaj de ĝi. Tie cent milimetroj respondas al la intenseco de pluvo po unu milimetro ĉiuminute.
Tiun ĉi someron(1) ni havis en la limoj de nia vetero-karto grandan nombron da ciklonoj, kiuj alkondukis pli malpli gravan difekton, sed la plej notindaj el ili estas tiuj, kiuj invadis Formoson.
La ciklono, kiu ruinigis la sudan regionon de Formoso la 26 kaj 27an de aŭgusto, aperis komence en la ĉirkaŭaĵo de Mariana insularo; ĝia centro, antaŭenirante unue okcidenten kaj poste nordokcidenten, trapasis la 26an je 10a horo matene la insulon Batan, kie la barometro malleviĝis ĝis sub 715 mm. kun vento, kies forto atingis 12 laŭ Beauforta skalo; en la nokto de la sama tago ĝi alvenis al la suda regiono de Formoso, preterpasis je 10a horo vespere Koŝun, kie la barometro malleviĝis ĝis 702.9 milimetroj; poste ĉiam konservante saman direkton ĝi trapasis formosan markolon kaj fine eniris en la ĥinan kontinenton la 27an posttagmeze.
Dum la pasado de la ciklono ekregis eksterordinara ventego kaj pluvego. La maksimuma rapido de vento estis ĉe Tajnan po 54.5 metroj ĉiusekunde; ĉe Koŝun malfeliĉe oni ne povis mezuri la maksimuman rapidon, ĉar la ventego forblovis la anemometron tuj post la momento, kiam oni observis je 7 h 45 m la rapidon de po 49.2 metroj ĉiusekunde; laŭ la direktoro de tiea observejo la maksimumo devis esti ne malpli ol po 70 metroj ĉiusekunde. La pluvokvanto estis de 508 mm. ĉe Koŝun, de 419 mm. ĉe Ako, de 396 mm. ĉe Banŝorjo, de 391 mm. ĉe Tajnan, k. t. p. Kontraŭ tia ventego kaj pluvego nenio povis kontraŭstari: arboj, pontoj, muroj, domoj deradikiĝis, disfalis, dispeciĝis; unuvorte ĉio ruiniĝis kaj nur ekregis plena ĥaoso. Laŭ oficiala raporto oni havis: 140 homojn mortiĝintajn, 300 vunditajn kaj 40 perdiĝintajn; 382 brutojn mortiĝintajn kaj 637 perdiĝintajn; 13794 domojn tute disfalintajn kaj 22163 duone disrompitajn; 221 pontojn falintajn k. t. p.
Jen kelke da observitaĵoj meteorologiaj :
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Koŝun | Tajnan | Hokoto | Tajĉu | Tajhoku | Kilung | ||
| Minimuma aeropremo |
} | 702.9 | 726.8 | 735.7 | 736.2 | 743.5 | 744.9 |
| Maksm vento m/s | (49.2) | 54.5 | 23.5 | 10.3 | 21.8 | 17.1 | |
Dum la ruiniga ventego kaj pluvego ekregis sur la suda regiono, tre varma kaj tre seka vento tute notinda okazis ĉe Tajĉu, urbo kuŝanta je la distanco de*6 120 km. norde de Tajnan. Tre favora estas la landformo de Formoso por naskiĝo de tia fenomeno, simila je la foehn de Svisujo, ĉar ĉi tie ankaŭ kuŝas, laŭ longe de la insulo, t. e. de nordo suden, grandaj montaj ĉenoj, kies pintoj en diversaj lokoj staras ĉirkaŭ 4000 metroj alte super la marnivelo. Ĉe Tajto la fenomeno okazas preskaŭ ĉiufoje, kiam ciklona centro sin trovas sur la maro nordoriente de Formoso; ankaŭ ĉe Tajĉu, se ne tiel ofte kiel ĉe Tajto, okazas la sama, kiam ciklona centro kuŝas sur la sudokcidenta maro, sed ĝis nun ĝi neniam estis tiel disvolvita kiel ĉi tiun fojon. De la noktomezo ĝis la sesa horo matene la temperaturo konstante leviĝis kaj atingis la maksimumon 34°.1 je kelke da minutoj post la sesa, en la momento, kiam oni ordinare havas la minimumon. La vento estis ne forta sed tre seka, oni sentis kvazaŭ alblovata de flamo; paperaĵoj, lignaĵoj, ĉio sekiĝis, ĉio krakis; nur de la momento, kiam la vento turniĝis al sudo, la temperaturo iom post iom malleviĝis kaj la aero iom malsekiĝis. Feliĉe estas, ke la fenomeno kaŭzis nenian malbonon.
Post kvar tagoj de la momento, kiam la suda regiono suferis de la ruiniga ciklono, nova ciklono ankoraŭ invadis la nordan regionon de Formoso. Tiu ĉi ciklono ankaŭ venis de la ĉirkaŭaĵo de la insularo Mariana, antaŭenirante unue WNW'n kaj poste okcidenten ĝi preterpasis la 31an de aŭgusto je la 3a horo posttagmeze la insulon Iŝigakiĵima, kie la barometro malleviĝis ĝis 704.3 mm. kaj la vento montris eksterordinaran rapidon de po 59 metroj ĉiusekunde; dum la nokto ĝi trapasis la ekstremnordan regionon de Formoso kaj fine ĝi eniris la 1an de septembro en la ĥinan kontinenton. Tiun ĉi fojon en Formoso la vento estis ne tiel forta kiel antaŭ nelonge en la suda regiono, la maksimuma rapido estis nur po 41 metroj ĉiusekunde, sed oni havis tute eksterordinare fortan pluvegon. En ok lokoj de la meza regiono unutaga kvanto da pluvo estis pli ol 400 milimetroj, en tri lokoj pli ol 800 mm., la maksimuman kvanton de*7 964 mm. oni observis ĉe Gotajho. Estas do ne mirinde, ke ĉie okazis eksterordinara superakvego, kiu kaŭzis grandegan difekton. Laŭ oficiala raporto oni havis: 305 homojn mortiĝintajn, 378 vunditajn, 190 perdiĝintajn; 10983 brutojn mortiĝintajn, 3574 perdiĝintajn; 13829 domojn tute disfalintajn, 13321 duone disrompitajn, 1581 forportitajn de akvo; 90 pontojn disfalintajn, 52 rompitajn, 521 forportitajn de akvo, k. t. p.
Jen kelke da observitaĵoj meteorologiaj:
| ĉe Kilung. |  |
ĉe Tajhoku. | ||||||
| horo | Barometro | Vento | Barometro | Vento | ||||
| Direk. rap. m/s | Direk. rap. m/s | |||||||
| 31a | T.M. | 741.9 | N | 25.7 | 743.2 | WNW | 15.2 | |
| 1p | 740.9 | NNW | 26.6 | 742.1 | WNW | 18.8 | ||
| 2p | 739.8 | NNW | 27.1 | 741.5 | NW | 11.5 | ||
| 3p | 738.7 | NNW | 28.4 | 740.1 | NW | 11.0 | ||
| 4p | 737.0 | NNW | 30.7 | 739.1 | WNW | 18.8 | ||
| 5p | 735.4 | NNW | 35.3 | 737.2 | WNW | 21.8 | ||
| 6p | 733.2 | NNW | 38.3 | 736.1 | WNW | 26.5 | ||
| 7p | 730.6 | NNW | 32.4 | 733.5 | WNW | 26.8 | ||
| 8p | 726.5 | NNW | 31.0 | 731.6 | WNW | 29.8 | ||
| 9p | 721.5 | N | 41.1 | 726.9 | WNW | 32.3 | ||
| 9½p | 721.3 | NNE | 16.5 | — | — | — | ||
| 10p | 722.0 | NNE | 13.2 | 723.2 | NW | 24.0 | ||
| 10½p | — | — | — | 723.1 | WNW | 8.3 | ||
| 11p | 726.0 | E | 8.9 | 723.7 | N | 6.5 | ||
| N.M. | 730.3 | E | 18.8 | 727.2 | NNE | 7.0 | ||
| 1a | 1a | 731.7 | ENE | 15.8 | 729.3 | NNE | 19.3 | |
| 2a | 731.8 | E | 14.8 | 729.8 | NNE | 19.5 | ||
| 3a | 731.8 | E | 12.6 | 730.3 | NNE | 19.0 | ||
| 4a | 731.9 | E | 10.6 | 730.6 | NNE | 15.2 | ||
(1) En la jaro 1911. — Red.
Pri tiu ĉi temo Dro J. Ŭada, direktoro de la meteorologia observatorio de Ninsen (Ĉemulpo) parolis antaŭ ni en la aprila kunveno de nia societo. La parolado estas japane donita en tiu ĉi numero kaj ni volas ekstrakti el ĝi kelke da tre gravaj kaj interesaj.
En la jaro 1899 kiam mi por unua fojo vizitis Koreujon, diras Dro Ŭada, mi vane penadis informiĝi pri la stato de meteorologio kaj astronomio en Koreujo. Poste marton 1905 mi povis vidi per la afableco de Dro Sidehara, tiama konsilanto ĉe la ministrejo de l' publika instruado de Koreujo, la observatorion de Seulo (ĉefurbo de Koreujo), kies direktoro estis Sro Li-ton-ŝu, kiu tre afable akceptis nin. Kio min miregigis, estis malnovaj astronomiaj instrumentoj kaj precipe tre malnova pluvometro. Mi demandis la devenon de tiuj instrumentoj al la direktoro, kiu ne povis doni precizan daton. Depost tiu momento mia deziro informiĝi la malnovan staton de astronomia kaj meteorologia observado en Koreujo pli kaj pli grandiĝis.
Dume mi ofte vojaĝis en la interno de Koreujo kaj vidis tie kaj alie malnovajn pluvometrojn kaj inter ili unu, kiu portas sur si la daton 1770; tio pruvas, ke almenaŭ en la jaro 1770 oni jam komencis mezuri pluvon eĉ en provinco. Cetere mi aŭdis de Dro Sidehara, ke en la libro Bunken-Biko oni trovas, ke en la jaro 1441 la reĝo Sejso konstruigis pluvometron, sed mi dubis, ke tiel fruan tempon oni jam pripensis pri tia instrumento.
Tamen tre feliĉe por scienco la anekso de Koreujo al nia lando tute malkovris la aferon; en tiu okazo transiris en nian registaron ĉirkaŭ 50000 volumoj da gravaj kaj interesplenaj manuskriptoj, kiuj enfermite en la reĝaj magazenoj eterne ne povus veni en taglumon. Inter la plej multekostaj por ni dokumentoj estas:
A) Liĉo-Recsej-ĵicuroku (Vera historio de la dinastio de Li). Ĝi konsistas el mil du cent kelkaj volumoj kaj enhavas tutajn dokumentojn de ĉirkaŭ 500 jaroj depost la komenco de la dinastio. Mankas al ĝi nur dek kelkaj volumoj.
B) Ŝosejin-Nicki (Taglibro de la ĉambelanejo). Al ĝi mankas volumoj por unuaj ĉirkaŭ 200 jaroj, sed kiu ankoraŭ restas, konsistas el ĉirkaŭ 3000 volumoj.
C) Nicsejroku (Taglibro de la kabineto). Al ĝi mankas tre multaj volumoj, sed kiu ankoraŭ restas el 2300 volumoj.
Krom tio mi ankoraŭ akiris taglibrojn de la observatorio; la konservado de ili neniel estas perfekta, malgraŭ tio ili estas por ni multekostaj.
Nun tute ne estas plu diskuteble, ke en Koreujo oni komencis mezuri pluvokvanton jam en la jaro 1441, ĉar oni ja legas en la vera historio de Sejso Vol. XCIII la reĝan ordonon eldonitan je aprilo 1441, kiu diras:
La ĝisnuna pluvomezuro ne estis perfekta, tial Ni fiksas novajn regularojn. Jen:
La pluvometro uzota en la ĉefurbo estu cilindro el fero fandita, kies alteco estas unu futo kaj kvin coloj kaj la diametro sep coloj laŭ la futo de Ŝu. (Komparinte tiun futon, kiu restas en la observatorio, kun metro mi trovis, ke ĝi ĝuste egalas 200 milimetrojn).
En la korto de l'observatorio oni konstruu piedestalon kaj sur ĝi sidigu la cilindron.
Ĉiufoje kiam pluvos, la kompetenta oficisto observadu la fenomenon, notu detale la momenton de la komenco kaj fino de la pluvofalo, mezuru fine la profundecon de l' akvo per la mezurilo dividita en lineoj.
La raporto tuj devas esti adresita al la reĝo.
La saman cilindron el fero kune kun la mezurilo oni sendu al ĉiuj provincestroj, por ke ili povu produkti laŭ modelo konvenajn pluvometrojn el porcelano aŭ bakita tero por disdoni al la provinco.
La estro mem notu la komencon kaj finon de la pluvo kaj mezuru la profundecon de l'akvo en la ilo.
La taglibrojn ili konservu al si, sed la raporto tuj devas esti sendita al la reĝo.
Ĉu oni ĉiam regule mezuris la pluvokvanton je antaŭfiksita horo? La taglibroj montras al ni, ke oni mezuris ĝin unufoje jen en 2 horoj, jen en 4 horoj, jen en 24 horoj laŭ la forteco de pluvo.
Forlasante flanken la jarojn, en kiuj la observadoj ne estas kompletaj, mi povis utiligi 135 jarojn por kalkuli pluvokvanton kaj 266 jarojn por pluvotago. La rezultato tiel ricevita estas donita en jena tabelo:
| Jan. | Feb. | Mart. | Apr. | Maj. | Jun. | Jul. | Aŭg. | Sept. | Okt. | Nov. | Dec. | Jaro. | |
| mm | mm | mm | mm | mm | mm | mm | mm | mm | mm | mm | mm | mm | |
| Kvanto | 5.7 | 9.2 | 32.6 | 69.1 | 81.9 | 127.9 | 347.0 | 265.1 | 126.8 | 46.2 | 35.4 | 15.1 | 1162.0 |
| Tagoj | 2.4 | 2.5 | 3.8 | 4.9 | 5.1 | 6.0 | 10.9 | 8.9 | 5.5 | 3.7 | 4.4 | 3.5 | 61.6 |
Ĉar la kutimo estis ne raporti al la reĝo pluvojn, kies kvanto ne atingis lineon t. e. 2 milimetroj, mi ne povas certiĝi, ĉu oni konsideris kiel pluvotagoj ĉiujn tagojn, en kiuj la pluvo falis, aŭ nur tagojn, en kiuj oni povis mezuri pluvon.
Cetere komparinte la observitaĵon (A) de la korea observatorio kun la observitaĵoj (B) faritaj en sama epoko de eŭropanoj aŭ japanoj mi trovis jenan rezultaton:
| Jaro | Pluvokvanto | Pluvotago | ||||
 |
 |
|||||
| A | B | A/B | A | B | A/B | |
| 1888 | 656mm | 845mm | 0.78 | 42 | 85 | 0.49 |
| 1890 | 854mm | 1105mm | 0.77 | 63 | 109 | 0.58 |
| 1907 | 658mm | 863mm | 0.76 | 51 | 130 | 0.31 |
Kiel oni devus atenti, la nombroj de la korea observatorio estas tro malgrandaj. Supozante, ke tiu ĉi konstanta rilato ĉiam ekzistis, mi alportis korektojn al la supre donita tabelo kaj ricevis jenan rezultaton kiu povus esti normala valoro:
| Jan. | Feb. | Mart. | April. | Maj. | Jun. | Jul. | Aŭg. | Sept. | Okt. | Nov. | Dec. | Jaro. | |
| mm | mm | mm | mm | mm | mm | mm | mm | mm | mm | mm | mm | mm | |
| Kvanto | 7.3 | 12.9 | 40.6 | 90.9 | 104.4 | 168.6 | 442.5 | 338.0 | 167.0 | 59.0 | 47.7 | 19.2 | 1498.1 |
| Tagoj | 4.8 | 5.2 | 8.9 | 12.8 | 13.9 | 16.1 | 28.9 | 23.9 | 15.2 | 10.0 | 11.3 | 7.4 | 158.4 |
Plue Dro Ŭada citas ankaŭ kelkajn notindajn pluvojn:
| Granda | jarsumo : | 2582mm en 1821, 2270mm en 1787. |
| Granda | monatosumo : | 1282mm en Julio 1821, 832mm en Julio 1787. |
| 322mm en 24 horoj en 16–17 Aŭg 1833 | ||
| 292mm en 14 horoj en 17 Julio 1855 | ||
| 170mm en 4 horoj en 1 Julio 1798 | ||
El la ciklonoj, kiuj vizitis nian regionon dum la monato de julio,(2) ni citos du tre rimarkindajn.
La unua estas tiu, kiu difektis la Jaejama-insularon. Aperinte la 14an en la maro inter la Ogasaŭara-insularo kaj la Mariana, kaj moviĝinte preskaŭ okcidenten, la ciklono preterpasis la Jaejama-insularon la 18an kaj eniris en la orientan maron; tie ĝi ŝanĝis la vojdirekton, iris nordorienten kaj atingis la 20an la nordan parton de Kjuŝu, kie ĝi fine malaperis. Ĉe la meteorologia observatorio de Iŝigakiĵima oni observis: minimuma barometro 733.7mm. je la 11a matene; maksimuma rapideco de vento po 53.0 metroj ĉiu sekunde; dum kvin horoj la rapideco de vento ĉiam estis pli granda ol po 50 metroj ĉiu sekunde.
Tiu ĉi ciklono estas precipe rimarkinda pro tio, ke surtere oni povis vidi la tiel nomitan ciklonokulon, kiun nur maristoj malofte vidis. Mi citos kelke da raportoj pri tio.
Sinjoro J. Ohama, loĝanto de la insulo Hateruma, kiu sin trovas en 58 kilometroj de la observatorio de Iŝigakiĵima sudokcidenten, skribis al ni:
La NE vento, kiu regis en la insulo Hateruma de antaŭ kelkaj tagoj iom plifortiĝis la 17an; la sekvantan tagon ĉirkaŭ la 8a matene ĝi subite fariĝis NW uragano kaj komencis skui dometojn, frakasi palmojn kaj aliajn facile rompeblajn arbojn. Je la 9a ĝia intenseco ankoraŭ pligrandiĝis: la ventego forblovas tegmentojn, fenestrojn; ĝi rompas, elradikigas fortikajn arbojn. Krom tio la pluvo estis fortega, ĝi kvazaŭ disverŝiĝis kaj ekregis tia mallumo, ke oni povas nenion distingi ĉirkaŭ si. La terura fenomeno tamen subite malaperis kvazaŭ per sorĉo kelkajn minutojn antaŭ la 10a: la vento tute kvietiĝis, la nuboj disflugiĝis, kaj eĉ la suno aperis kaj varmege brilis; sed la silento ne povis longe daŭri. La ĝisnuna terura bruado de ventego estis baldaŭ anstataŭata de lamentaj krioj de patrinoj vokantaj perdiĝintajn infanojn aŭ de infanoj serĉantaj gepatrojn. La indiĝenoj sciantaj per sperto, ke, kiam la uragano subite ĉesis, oni ofte devas atendi novan ventegon multe pliteruran ol la ĵus pasintan, profitis tiun ĉi kvietan tempon por apliki ĉiujn eblajn rimedojn, kiuj helpus kontraŭstari kontraŭ baldaŭ venonta ventego: oni alnajlas, alligas fenestrojn, pordojn; oni kovras tegmenton per reto, oni almetas apogfostojn al domo, por ke ĝi ne renversiĝu. Efektive post dudek minutoj da kvieto la uragano reaperis kun tia forto, ke ĝi multfoje superas la antaŭan, kaj daŭris ĉirkaŭ unu kaj duono horojn. La plimulto da domoj disfalis; amaso da arboj disrompitaj aŭ elradikigitaj kuŝis en ĥaoso sur la tero kaj baris la vojon tiel, ke la komunikado estas tute neebla. Arboj savitaj de elradikigo staras sen folioj nek branĉoj kiel mastoj. Feliĉe estas, ke la nombro de*8 homoj vunditaj aŭ mortigitaj ne estis granda kompare je la graveco de la katastrofo: oni trovis nur du mortintojn sub domoj disfalintaj. Ne multe ankaŭ estis la perdo de brutoj, sed tie kaj ĉi tie kuŝis multe da mortintaj korvoj.
La raporto de la lernejestro de la insulo Jonakuni, sinjoro Hazama, montras al ni, ke tie ankaŭ oni vidis la ciklonokulon. Jen la raporto:
Ni havis jam de la 15a de julio maltrankvilan veteron kun NE vento. La 18a tagiĝis kun forta, norda vento, kiu je la dua horo posttagmeze fariĝis vera uragano akompanata de pluvego. La ruiniga ventego, kiu forblovis tegmentojn, rompis aŭ elradikigis arbojn, subite malfortiĝis je la kvina horo; kun la vento ankaŭ ĉesis la pluvo kaj la blua ĉielo aperis. Tamen tiu ĉi trankvileco ne daŭris pli ol duonhoron: la vento turniĝis maldekstren kaj fariĝis SE uragano, kies forto atingis la supron inter la 6a kaj 7a horo vespere. Grandnombraj estis arboj rompitaj aŭ elradikigitaj, multe da domoj disfalintaj; nedifektitajn tegmentojn oni trovis nenie. Mi trovis sur la bordo tute senŝeligitajn arbojn; kredeble ili estis skrapitaj per sableroj disblovitaj de ventego.
La dua ciklono estas tiu, kiu invadis Formoson la 19an. Tiu ĉi ciklono sin montris, la 13an, en malproksima maro sudoriente de Filipino kaj moviĝinte nordokcidenten ĝi atingis, la 19a frumatene, Formoson ĉe Tajto, kie la barometro malleviĝis ĝis 738.3 mm. je la 6a horo matene, kaj trapasis la insulon por eniri en la formosan markolon. Post kiam ĝi trapasis sinsekve la orientan maron, la flavan maron, nordan Koreujon, ĝi fine malaperis en la norda parto de la japana maro.
Tiu ĉi ciklono estas rimarkinda pro tio, ke ĝi estis akompanata de eksterordinara pluvego. Jen la pluvokvanto mezurita en la du tagoj la 18–19a: 1610 mm. ĉe Jojorin: 859 mm. ĉe Ĉikutoki; 727 mm. ĉe Koŝun. Kompreneble tia pluvego kaŭzis teruran superakvon kaj gravajn difektaĵojn en Formoso. Laŭ la raporto de la formosa policestro estis:
33 mortintaj, 13 grave vunditaj, kaj 70 perdiĝintaj homoj; 838 mortintaj kaj 5476 perdiĝintaj brutoj; 2115 plene disfalintaj, 2488 duone falintaj kaj 878 forportitaj de akvo domoj; 9 km. da fervojoj forportitaj de akvo.
(2) En la jaro 1913. — Red.
Tiun ĉi monaton en la kontinento jam ofte sin disvolvis anticiklonoj, sed ili ankoraŭ ne estis persistaj kaj rapidis orienten, trapasante Japanujon. Ilin sekvis ankaŭ kontinentaj ciklonoj aperintaj en supra valo de Jance-rivero kaj kaŭzis ventegon kaj pluvegon en Flava Maro, Koreujo, Japanmaro kaj norda Hokkajdo, sed feliĉe ili ne estis ruinigaj.
La plej altan aeropremon 775.7 oni observis en Siska la 31an kaj plej malaltan 725.3 en Ŝionomisaki la 1an. La mezaeropremo estis pli alta ol la normala en tuta Japanujo kaj precipe en suda insularo, kie troa ekarto estis pli ol 3 milimetroj.
La reganta vento estis N aŭ NW en Japanujo krom NWa marbordo, kie regis SEa vento; en suda insularo tamen ĝi estis NEa. La mezforto de vento estis preskaŭ normala; en centra Japanujo la ekarto estis iom troa, sed en aliaj lokoj iom manka. La plej forta vento observita estas po 43 m. ĉiusekunde; ĝi okazis la 1an en Cukubasan kaj Ŝionomisaki.
La meztemperaturo estis 24°—25° en suda insularo 18—19° en Ĥinujo; 16—17° en okcidenta parto de Japanujo, en Koreujo kaj norda Ĥinujo; 11—12° en centra Japanujo kaj 8—9° en Hokkajdo. Ĝi estis iom plialta ol la normala krom en centra Japanujo kaj suda marbordo, sed la ekarto ne estis granda. La absoluta maksimuma temperaturo superis 30° en suda insularo; 25° en propra Japanujo; 21° en Hokkajdo. Ĝi okazis ĝenerale en la fino de la dua dekado krom en sudorienta marbordo kaj Koreujo, kie ĝi aperis en la komenco de la monato. La absoluta minimumo jam malleviĝis ĝis -5° en Hokkajdo kaj eĉ ĝis -9° en Karafto, dum en propra Japanujo ĝi restis super nulo kaj en suda insularo ĝi eĉ superis 17°. La plej alta temperaturo estis 32°9 en Taihoku kaj la plej malalta -9.7 en Oĉiaj. La maksimumo ĝenerale aperis en la fino de la dua dekado sed en suda insularo je la komenco de la dua; la minimumo ĝenerale okazis en la tria dekado.
La temperaturo prezentis tri fazojn en tiu ĉi monato, kiu komencis kun manka ekarto. De la 5a ĝis la 7a, de la 16a ĝis la 20a, de la 27a ĝis la fino la temperaturo estis pli alta ol la normala kaj precipe la 20an kaj 27an. En ĉi tiuj du tagoj troa ekarto ĝenerale superis 5 gradojn kaj en multaj lokoj eĉ 7°. La plej granda ekarto manka okazis la 12an aŭ 21an; en Koreujo ĝi atingis 5°.
La pluvokvanto estis tre malabunda en la tuta regiono krom kelkaj partoj. Ĝenerale ĝi estis nur duono de la normala kaj en suda insularo eĉ nur triono aŭ kvarono. Tamen okcidenta parto de Koreujo, ĉirkaŭaĵo de Nagasaki, de Biŭa-lago kaj de Kamo estis tre riĉa je pluvo, en multaj lokoj la pluvokvanto atingis trioblon de la normala. La nombro de pluvotagoj estis iom pligranda ol la normala en NWa marbordo, sed malgranda en aliaj lokoj.
La sunbrildaŭro ĝenerale estis ĉirkaŭ 50% de la ebla daŭro kaj iom pligranda ol la normala.
Prujnon oni jam observis en diversaj lokoj eĉ en Kiuŝu. En propra Japanujo la unua prujno okazis tre frue, sed en norda regiono ĝi tre malfruiĝis.
Neĝon oni nur observis en Karafto kaj norda Koreujo. En Siska unua neĝo jam falis la 5an, en Koreujo la 20an, kaj ĝi okazis ĉie tre frue.
La 25an de majo(3) nia sismografo registris malproksiman tertremon. La unua antaŭtremado komencis je 11h 32m 24s matene laŭ japana centra tempo, t. e. tempo de 135a meridiano E de Greenwich, kaj post 14m 35s aperis la ĉefa tremado, kies amplitudo estas tiel granda, ke, se ĝi estus iomete pli granda, la plumo elirus el la registrilo. Ni ne dubas, ke tiu ĉi tertremo okazis en maro tre malproksima de lando aŭ en ia regiono preskaŭ senhoma, ĉar alie la gazetoj jam devas al ni alporti ian sciigon pri la de ĝi kaŭzita difektaĵo. Laŭ la sismografaj diagramoj de niaj observatorioj ni ne povas konkludi, ke ĝi okazis en la dezerto de centra Azio, ĉar la distanco, rilate je Koreujo, estas multe pligranda ol tio, kio rilatas je Formoso; sed pli verŝajne estas, ke ĝi okazis en hinda oceano inter Cejlono kaj Sumatro, ĉar tie sin reciproke tranĉas la kelkaj ĉiu observatorio kiel centro kaj kun distanco kalkulita kiel radio desegnitaj cirkloj. El ĉio ĉi tio ŝajnas al mi, ke mi povas meti la epicentron sur la lokon, kies geografia pozicio estas: ĉirkaŭ 10° N kaj 90° E. Cetere, sur la sekvanta paĝo sin trovas la observitaĵoj, kiujn mi ĝis nun kolektis:
| Loko | Horo de apero | Daŭro de antaŭ- tremado | Ĉefa tremado | Tuta daŭro | Distanco el obser- vatorio |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Daŭro | Maksimuma amplitudo | Periodo | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| I | II | I | II | III | I | II | III | I | II | III | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(3) En la jaro 1912. — Red.
Laŭ ĵurnaloj okazis, matenon de la 9a aŭgusto,(4) en ĉirkaŭaĵo de dardanela markolo tre forta tertremo, kiu detruis grandan nombron de*9 domoj kaj eĉ kaŭzis al centoj da popoloj la perdon de vivo.
Ĉi tie en Osaka, la sismografo tre klare registris la tremadojn. La unua antaŭtremetado komencis je 10h 41m 26s kaj daŭris 10 minutojn; tio donas por la distanco ĝis la epicentro 8900 k.m., kiu bone respondas al la efektiva. Ĉar la tremado bezonas ĉirkaŭ 10 m 40 s por sin propagi ĝis ni, en dardanela markolo ĝi devas esti okazinta je ĉirkaŭ 3 h 30 m matene (laŭ la meztempo de 30a grada meridiano, oriente de Greenwich).
La observitaĵoj de Osaka estas donitaj en jena tabelo:
| N-W tremado | N-S tremado | ||||||||||||
| Daŭro | Mez- periodo |
Mak. Ampl. |
Kies periodo |
Daŭro | Mez- periodo |
Mak. Ampl. |
Kies periodo |
||||||
| m | s | m | s | ||||||||||
| Antaŭ- tremetado |
 |
1 a | 10 | 00 | 6.0 | 0.06 | 7.2 | 10 | 00 | 6.0 | 0.06 | 7.0 | |
| 2 a | 10 | 58 | 7.1 | 0.17 | 9.6 | 10.58 | 7.1 | 0.26 | 14.4 | ||||
| Ĉeftremado |  |
1 a | 6 | 23 | 12.8 | 0.46 | 28.8 | 6.24 | 12.7 | 1.29 | .336 | ||
| 2 a | 7 | 48 | 19.5 | 1.70 | 21.6 | 7.48 | 2.63 | 2.05 | 2.88 | ||||
| 3 a | 10 | 41 | 19.7 | 4.62 | 20.2 | 10.51 | 19.7 | 4.56 | 2.40 | ||||
| 4 a | 16 | 31 | 15.0 | 1.70 | 17.8 | 16.14 | 17.8 | 3.55 | 2.30 | ||||
| 5 a | 19 | 00 | 14.2 | 0.17 | 15.4 | 19.33 | 16.8 | 0.17 | 1.82 | ||||
| 6 a | 19 | 55 | — | 0.04 | 1.54 | 20.34 | — | 0.05 | 1.68 | ||||
| Fintremetado | 54 | 32 | — | — | — | 57.48 | — | — | — | ||||
| Tuta daŭro | 2 h 35 m 48 s | 2 h 40 m 10 s | |||||||||||
(4) En la jaro 1912. — Red.
Okazas ne malofte, ke oni konstruas fervojon ne tre malproksiman de sisma observatorio, kaj domaĝo estas, se veturanta vagonaro povus kaŭzi tremadon al tero, sur kiu staras la observatorio. Tial mi entreprenis eksperimentojn por determini minimuman*10 distancon, trans kiu la influo de vagonaro ne povas atingi. Kompreneble tia tasko estus tute sensenca, se oni volus ĝin determini rigore, ĉar ĝi nepre dependas de la geologia strukturo de tero, tamen mi kredas, ke miaj eksperimentoj povas doni almenaŭ ĝeneralan ideon.
La instrumento, kiun mi uzis, estas simpla tremometro laŭ Prof. F. Omori kun centobla multiplikilo; ĝia propra periodo estis 3.3 sekundoj. La eksperimentojn mi faris en la kampo de la agronomia eksperimentejo ĉe Niŝigahara apud Tokio; la geologia strukturo estas diluva. La eksperimenta metodo estis: meti sismografon aŭ paralele aŭ perpendikle*11 je la fervojo, kaj serĉi la lokon, kie la instrumento sentas nenian influon de vagonaro.
Eksperimentoj de la 1a de oktobro 1913. —Mi metis la sismografon je la distanco 80 metroj de fervojo kaj movis*12 per malgranda elektra motoro ĝian tamburon; kiu turniĝis tre rapide sed regule kaj kviete. Veturanta vagonaro produktis tertremadon kaj la instrumento donis regulan kurbon. La kurbo komencas de relative*13 malrapida tremetado, kiu daŭris 7 sekundojn, ĝia periodo estis 0.3—0.5 sekundo: poste venas zigzago, kiun oni povas konsideri kiel ĉefa tremado, tiu ĉi parto kavas du maksimumojn kies periodo estas 0.2 sek. kun amplekso de 0.03 milimetro; ĝi finas kun tremetado, kies periodo estas 0.5—0.7 sek. Jen la resumo de observaĵo:
| Horo h m |
Pezo (tuno*14) | Daŭro | Maksimuma | Speco de Vagonaro |
||||||||||||||||||||||||||||
| Lokomotivo | Vagonoj | ŝarĝo | sumo | Komenca tremetado sek. |
ĉefa tremado sek. |
Fina tremetado sek. |
Periodo sek. |
Amplekso mm. |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
La pezo de la ŝarĝo estas pezo, kiam la vagonoj estas plene ŝarĝitaj; la efektiva pezo devas esti pli malgranda, eble de 10–20%.
Eksperimento de la 4a de Oktobro 1913. —Tiun tagon mi faris eksperimentojn en diversaj distancoj, sed mi nur citos unu el ili. Je la distanco 170 metroj de fervojo mi povis observi tertremadon aŭ ne, laŭ la speco de vagonaroj; jen la resumo:
| Horo h m |
Pezo | Rimarko | ||||||||||||||||||
|
||||||||||||||||||||
|
|
|
Konkludo :—De la eksperimentoj mi povas konkludi, ke la veturanta vagonaro donas al la apuda tertavolo regulan tertremadon kun mallonga periodo, kiu konsistas el ĉeftremado kaj komenc-kaj fintremetado, kaj ke la tremado ne povas transiri la distancon de 200 metroj, se la tero estas diluva.
Cetere, mi demandis al kelkaj meteorologiaj observatorioj, en kies proksimo sin trovas fervojo, ĉu ili sentas la influon de vagonaro, kaj ricevis jenajn respondojn:
| Observ. | Distanco de fervojo |
Influo de vagono |
Naturo de tero |
Rimarko | ||||||||||||||||||||||||||||||
|
|
|
|
|
Ĉar ĉiuj aferistoj, scienculoj ĝenerale, kaj precipe statistikistoj kaj meteorologoj*15 bezonas ĉiutage praktikajn kalkulilojn, mi volas konigi al la en orienta Azio larĝe disvastigitan, malnovan sed tre praktikan kalkulilon, SOROBAN'on. La ĉisube donitaj mallongaj priskriboj kaj klarigo tuj povus ilin konvinki, ke ĝi per simpleco de konstruo, sekve per malkareco de prezo(5), per facileco de manipulado, kvankam tre malnova, superas eĉ ĉiujn en niaj tempoj elpensitajn novajn kalkulilojn.
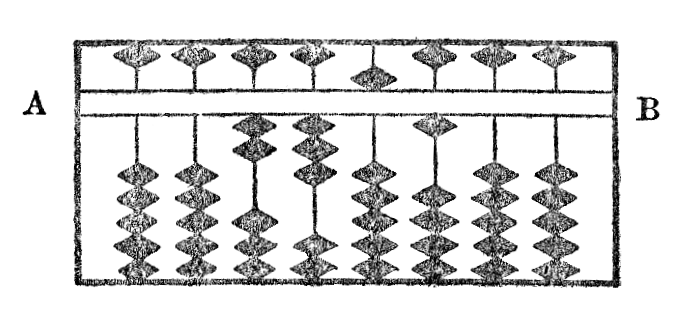
La sorobano konsistas el aroj da globetoj trairitaj de stangeto kaj tute similas je la en Eŭropo bone konata abako; la sola diferenco tamen estas el tio, ke ĉe sorobano la globetoj tiamaniere estas apartigitaj per baro AB en du grupoj, supra kaj malsupra, ke sur ĉiuj stangetoj sin trovas unu globeto en supra kaj kvin en malsupra parto. Ĉar ĉiu globeto supra valoras kvin unuojn, oni havas entute dek unuojn sur ĉiuj stangetoj.(6)
Por prezenti ciferon sur la ilo oni alpuŝas al la baro AB tiom da globetoj, kiom ĝi en si enhavas da unuoj. Por prezenti ian nombron sur la ilo sufiĉas nur, ke oni metas ciferojn unu post alia tute tiel, ke oni skribas tiun ĉi nombron per arabaj ciferoj.
Jen kelke da ekzemploj: la figuroj (Ia) & (Ib) prezentas respektive 2351 & 86409.
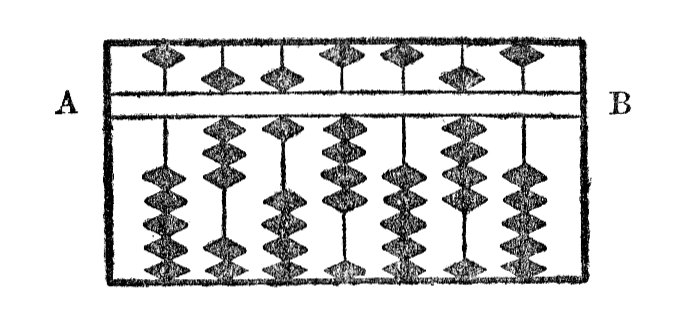
Supozante, ke oni bone komprenis la aranĝon de l' aparato, mi nun klarigos, kiel oni f'aras la kvar operaciojn.
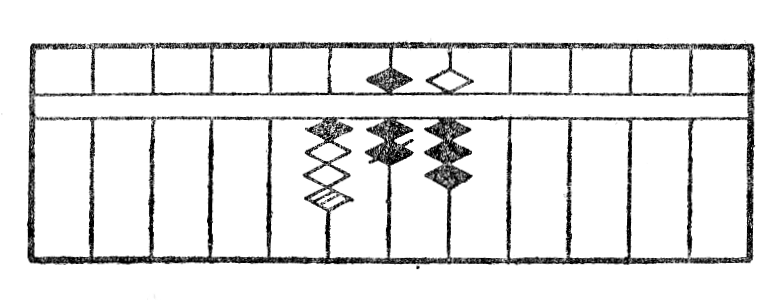
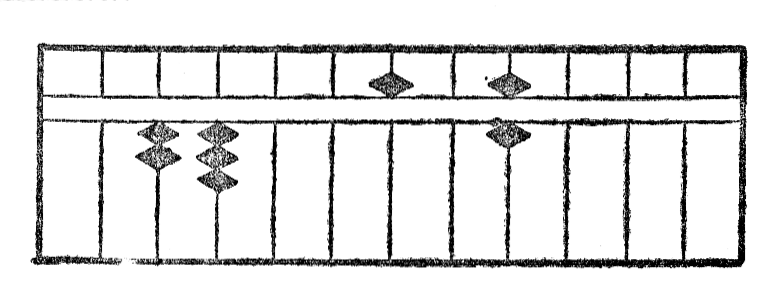
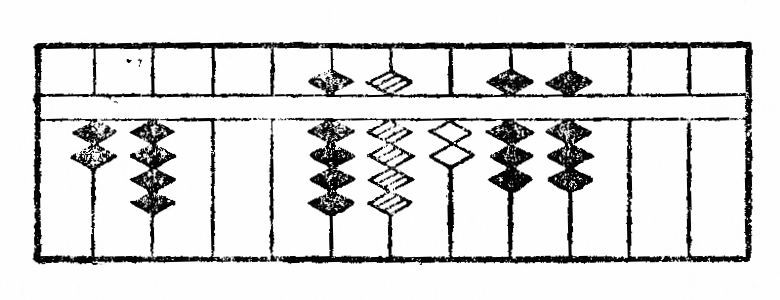
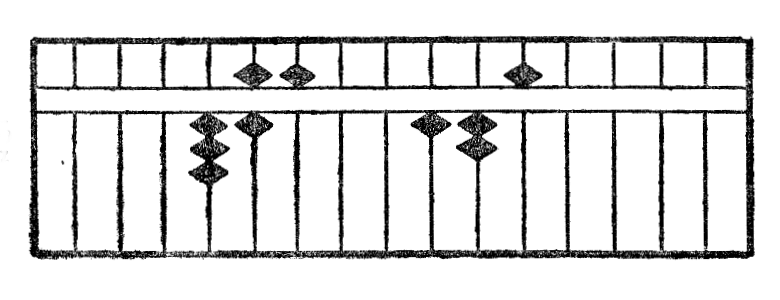
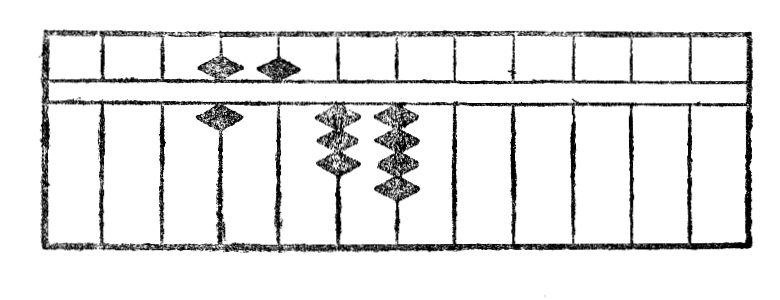
Por fari adicion per la sorobano sufiĉas nur, ke oni metas intersekve ĉiun nombron sur la ilo, la rezultato per si mem*17 aperas sur la tabulo. Estu ekzemple adicii 123 al 322; oni unue metas unu el du nombroj, ekzemple 123 (kiun mi prezentas per ◆) kaj poste 322 (kiun mi prezentas per ◇). La rezultato estas videble 445.
Rimarko I.—Kiam kvin globetoj malsupraj tute devas esti uzataj, oni ĉiam anstataŭigas ilin per unu globeto supra*19. La antaŭa figuro tiel prenas jenan formon:
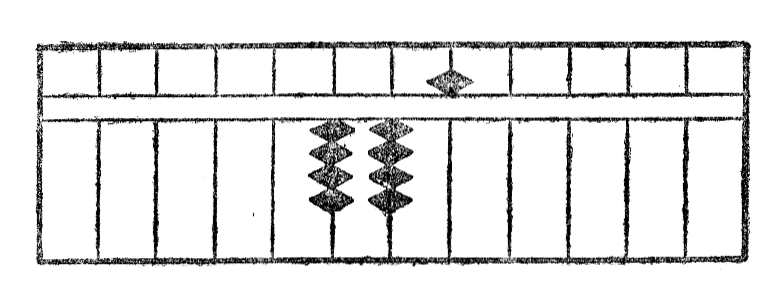
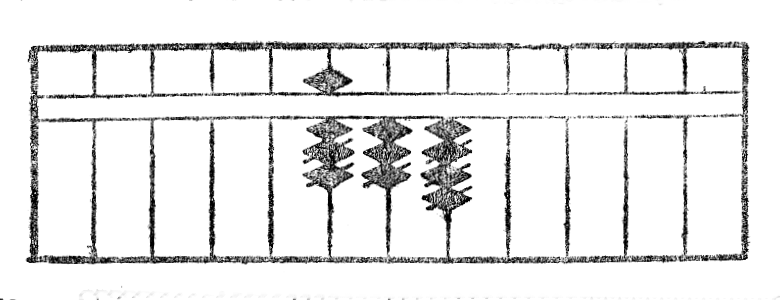
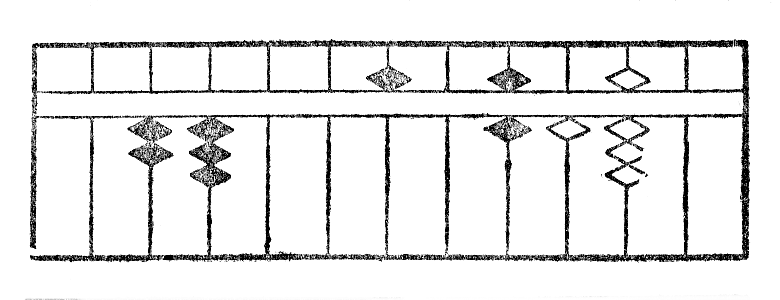
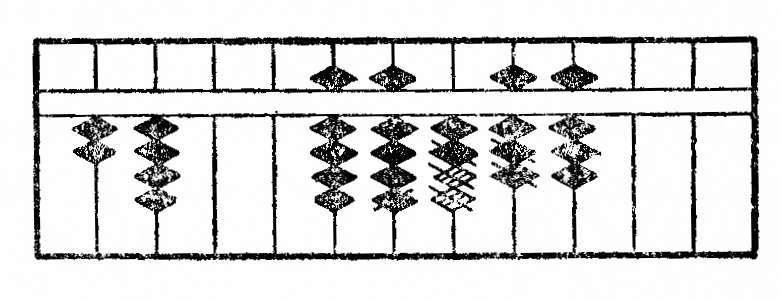
Rimarko II.--Kiam la sumo de du ciferoj superas dek, oni aldonas unu unuon al cifero sur la maldekstre apuda stangeto kaj deprenas de la cifero konsiderita la komplementon, rilatante je dek. Tial la adicion de 173 kaj 295 oni faras tiel, kiel jena figuro IV montras la procedon: La rezultato videble estas 468.
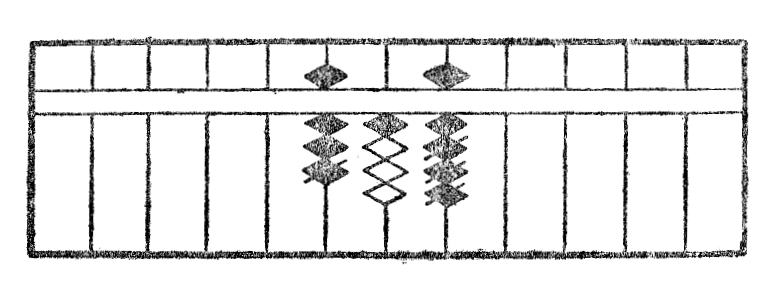
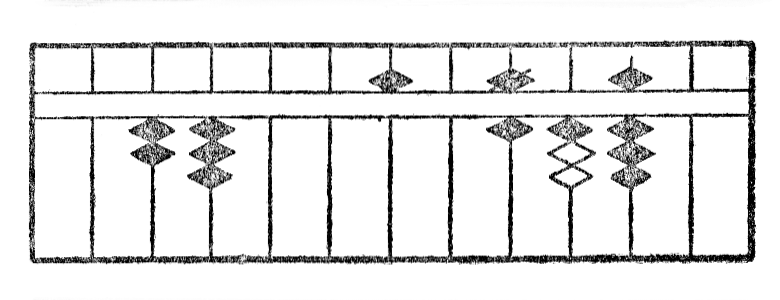
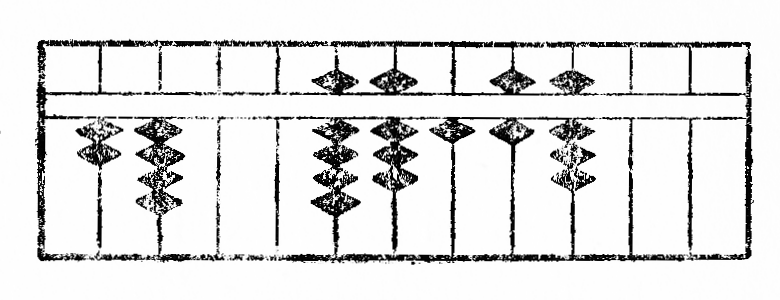
Por fari subtrahon*20 per la ilo, oni unue metas sur ĝin la pligrandan el du nombroj kaj deprenas de cifero sur ĉiu stangeto tiom da globetoj, kiom ĉiu cifero de la plimalgranda nombro enhavas da unuoj. La procedo por subtrahi*21 213 de 834 estas klare montrita*22 per la figuro V. La rezultato videble estas 621.
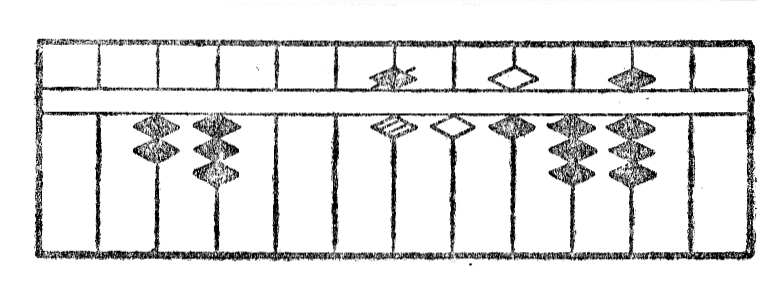
Rimarko.—Se sur iu stangeto sin ne trovas sufiĉe da globetoj per povi depreni la nombron deziritan, oni malpliigas de unu unuo la ciferon sur maldekstre apuda stangeto kaj aldonas al la cifero konsiderita la komplementon, rilatante je dek. La figuro VI montras la subtrahon*23 de 73 de 819. La rezultato estas videble 746.
Por fari multiplikon, kompreneble, estas necese, ke oni sciu parkere ĉiujn produtojn de du nombroj pli-malgrandaj ol dek. La multiplikanton oni metas en la maldekstran kaj la multiplikaton en la dekstran flankon de la ilo. La operacio ĉiam komenciĝas je la lasta (plej dekstra) cifero de la multiplikato kaj finiĝas je la unua (plej maldekstra).
Kiam la multiplikanto estas unucifera, la operacio estas tute simpla. Ĝi konsistas el tio, ke intersekve oni aliformigas ĉiujn ciferojn de la multiplikato en dekoj de produto kaj aldonas unuojn de produto al la dekstre apuda stangeto.
Ekzemploj: Estu multipliki 7 per 6. Oni aliformigas la multiplikaton 7 en 4, dekoj de la produto 42, kaj aldonas al ĝia dekstre apuda stangeto 2, unuoj de la produto. La figuro VIIa montras la unuan aranĝon de kalkulo kaj la fig. VIIb la rezultaton, kiu videble estas 42.
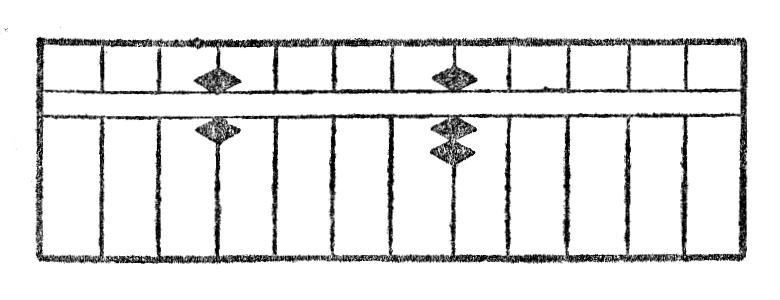
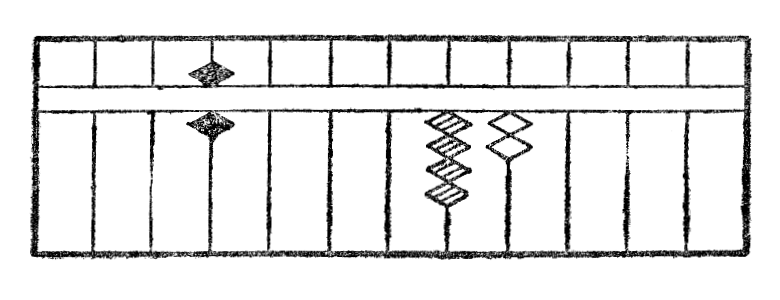
La operacio de la multipliko de 46 per 3 estas montrita per la figuroj VIII: la figuro VIIIa montras la unuan aranĝon de kalkulo; la fig. VIIIb partan rezultaton de la multipliko de la lasta cifero 6 per 3; la fig. VIIIc la finan rezultaton, kiu estas 138.
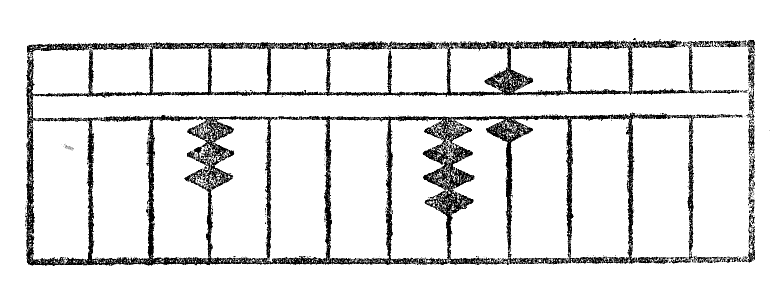
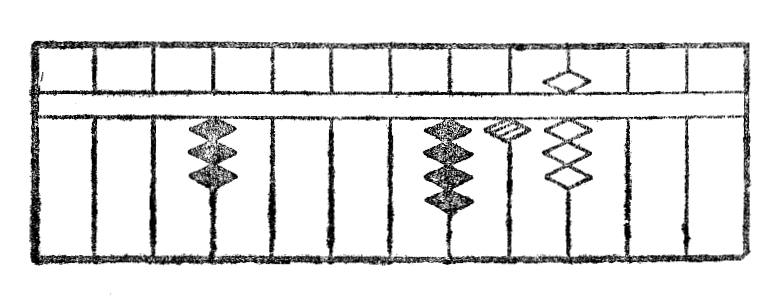
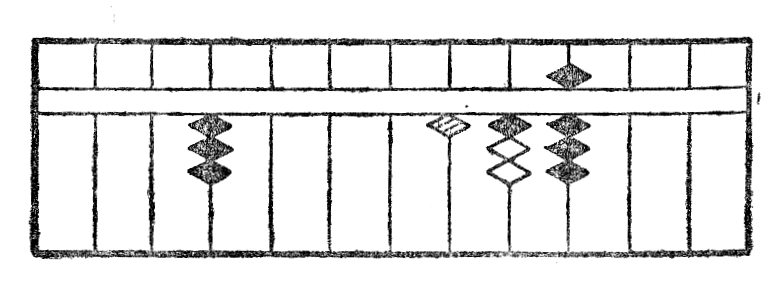
Konsideru infersekve unu el la ciferoj de multiplikato (oni ĉiam komencas je la lasta cifero) kaj multipliku ĝin per ĉiuj ciferoj de multiplikanto. Ĉiujn partajn produtojn tiel ricevitajn oni tiamaniere metas sur stangetoj, kiuj kuŝas en ĝia dekstra flanko, ke la dekoj de produto sin trovu sur la stangeto, kies rango rilatante je la stangeto konsiderita egalas tiun de la cifero konsiderita de la multiplikanto, rilatante je ĝia unua cifero; la multiplikon per tiu ĉi lasta oni faras tiel same, ke se la multiplikanto estus unucifera.
Estu ekzemple multipliki 506 per 23. Oni multiplikas intersekve per 3 kaj 2, unue la lastan ciferon 6, poste la duan 0 (kompreneble, kion oni neniam faras en praktiko.), fine la unuan 5. La figuro IXa montras la unuan aranĝon de kalkulo; fig. IXb la partan rezultaton de la multipliko de 6 per 3; fig. IXc la saman per 2; fig. IXd la rezultaton de multipliko de 5 per 23 kaj samtempe ankaŭ la finan rezultaton, kiu videble estas 11638.
Rimarko.—Kiam la multiplikanto konsistas el tre multe da ciferoj, oni komencas multipliki ciferon konsideritan de multiplikato per la dua cifero de multiplikanto, poste per la tria, k. t. p. ĉiam irante dekstren ĝis la lasta cifero, kaj oni fine revenas al la unua. Tiamaniere oni havas malmulte da ŝanco erari de la loko, kien oni devus meti partajn produtojn.
Sur kiu stangeto sin trovas la unuoj de la produto? Jen estas la regulo por trovi ĝian lokon:
Regulo. —De la stangeto, sur kiu kuŝas la unuoj de multiplikato paŝu dekstren tiom da stangetoj, kiom la multiplikanto enhavas da ciferoj en ĝia entjera parto, tie vi trovos la unuojn de la produto.
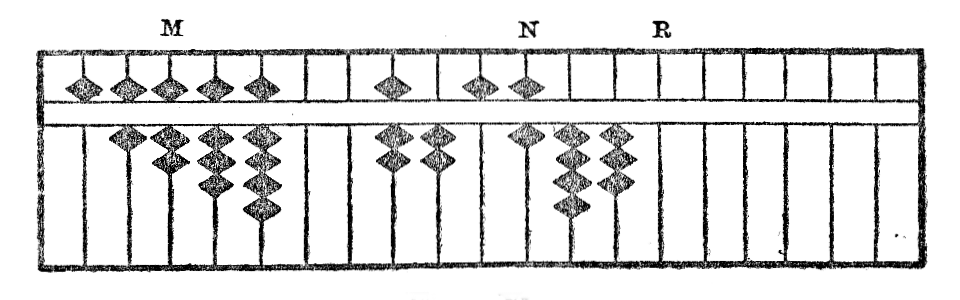
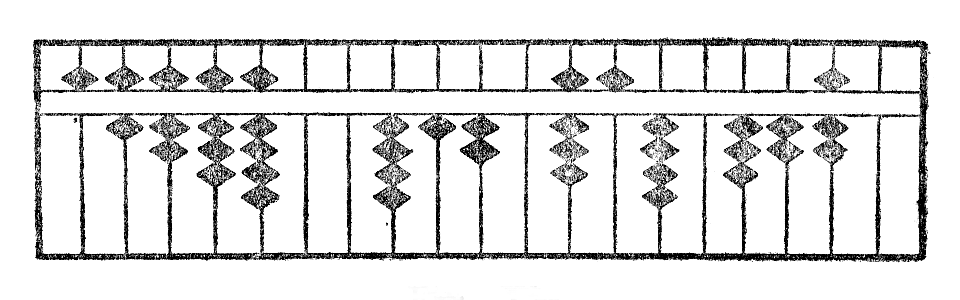
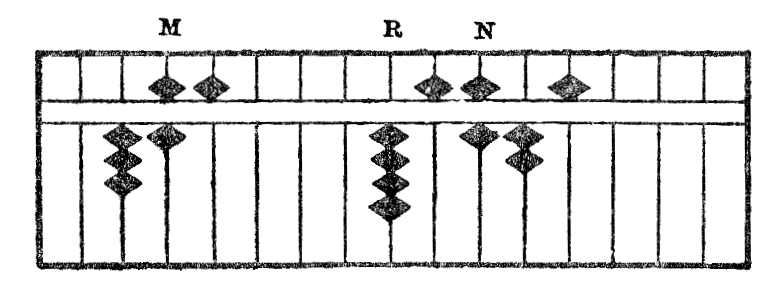
Ekzemple, se oni multiplikas 7256,43 per 567,89, kie sin trovos la unuoj de la produto?
Estu M kaj N la stangetoj, sur kiuj respektive kuŝas la unuoj de multiplikanto kaj multiplikato, vi trovos la unuojn de produto sur la stangeto R, dekstren tria de N. Kiel oni vidas sur la figuro Xb, la rezultato estas 4120854,0327.
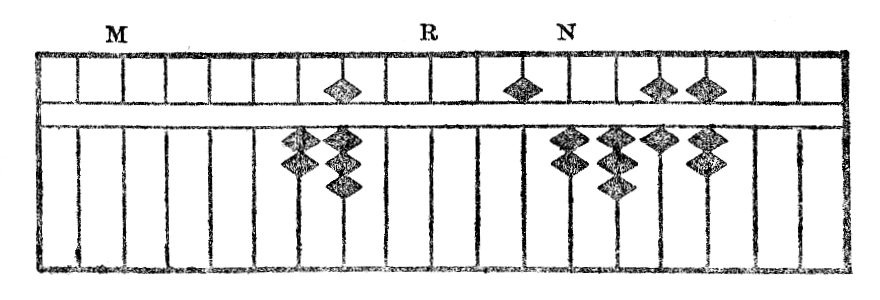
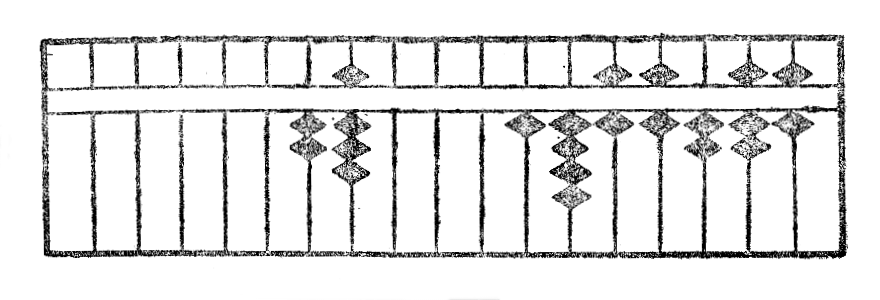
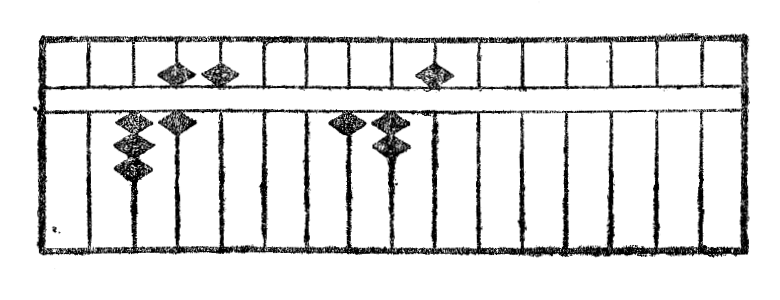
Kiam la multiplikanto ne havas entjeron, paŝu de la unuoj de la multiplikato maldekstren tiom da stangetoj, kiom ĝi havas da nuloj post komo, tie vi trovos la unuojn de la produto.
Ekzemple, en la multipliko de 52,367 per 0,00028 la unuoj de produto sin trovos sur la stangeto R, la maldekstre tria de la stangeto N, sur kiu kuŝas la unuoj de multiplikato. La produto ricevita estas videble 0,01466276.
Por fari dividon per la ilo oni nepre devas scii parkere la nombrojn sur jena tabelo, nomita dividtabelo.
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
La formado de tiu ĉi tabelo estas tre simpla. Konsideru la dividon de multobloj de dek per ĉiu el naŭ unuaj entjeroj kaj prenu la kvocienton entjeran kiel dekoj kaj la reston kiel unuoj, vi trovos la nombrojn de la tabelo.
La dividanton oni ĉiam metas en la maldekstran kaj la dividaton en la dekstran parton de la ilo. La divido komenciĝas je la unua cifero de la dividato, poste oni dividas la duan, la trian, k t p., ĉiam irante dekstren.
La operacio konsistas el tio, ke oni aliformigas la ciferon konsideritan en dekoj de nombro el la dividtabelo kaj aldonas al ĝia dekstre apuda stangeto la unuojn.
Se la cifero dividota estas pligranda ol la dividanto, oni malpliigas ĝin de nombro egala je la dividanto kaj pliigas de unu unuo la nombron sur ĝia maldekstre apuda stangeto, kaj oni ripetas saman operacion, ĝis ĝi fariĝas pli malgranda ol dividanto.
Estu ekzemple dividi 322 per 7. La operacio estas montrita per sekvantaj figuroj XII. La figuro XIIa montras la unuan aranĝon de kalkulo. Unue ni dividas 3 per 7: por tio ni aliformigas 3 en 4, dekoj de 42 kaj aldonas 2 al la sekvanta cifero 2 (fig. XIIb).
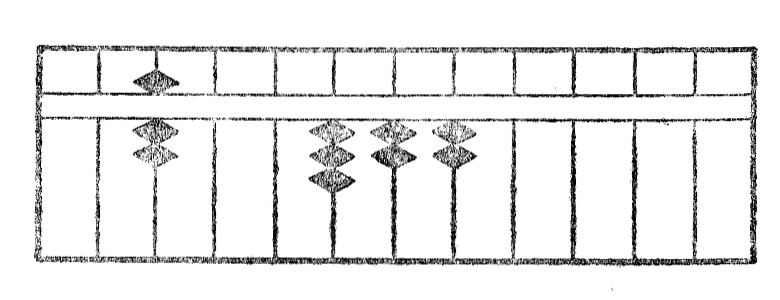
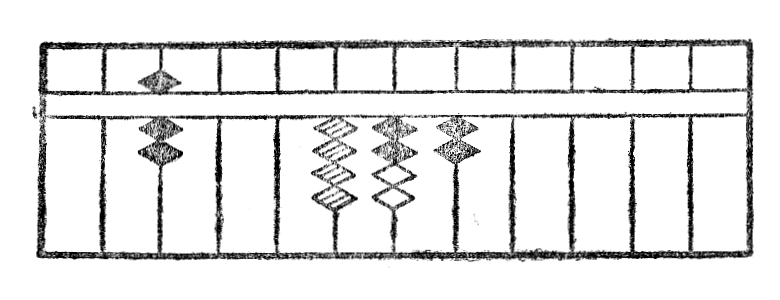
Ni denove aliformigas duan ciferon 4 en 5, dekoj de 55 kaj aldonas 5 al la sekvanta cifero (fig. XIIc). Ĉar la nova tria cifero 7 estas egala je la dividanto, ni deprenas de ĝi unu fojon 7 kaj aldonas unu unuon al ĝia maldekstre apuda stangeto (fig. XIId). La resto estante nula, la operacio estas do finita, kaj la kvociento estas videble 46.
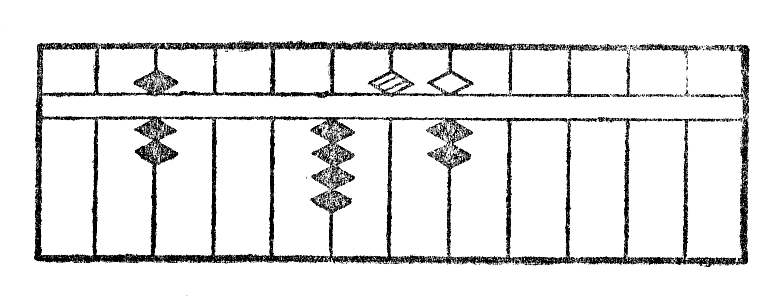
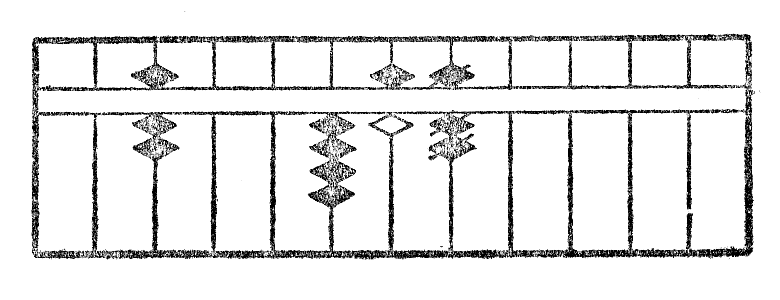
Unue oni dividas la unuan ciferon de la dividato per la unua de dividanto tute tiel ke se la dividanto estus unucifera, poste oni deprenas de la unuan kvocienton sekvantaj ciferoj partajn produtojn de la ĵus ricevita kvociento per ĉiuj ciferoj de la dividanto, krom la unua. Por fari tiujn ĉi subtrahoj*24 oni nur zorgu, ke la unuoj de la parta produto per la dua cifero de dividanto sin trovu sur la kvociento dekstre dua stangeto, ke la unuoj de la produto per la tria sur la tria k. t. p. Kiam oni finis tiujn ĉi subtrahojn*25, oni rekomencas saman operacion sur la dua cifero de dividato kaj sur la tria k. t. p.
Ekzemple: Estu dividi 1296 per 36. La operacio estas montrita per la figuroj XIII.
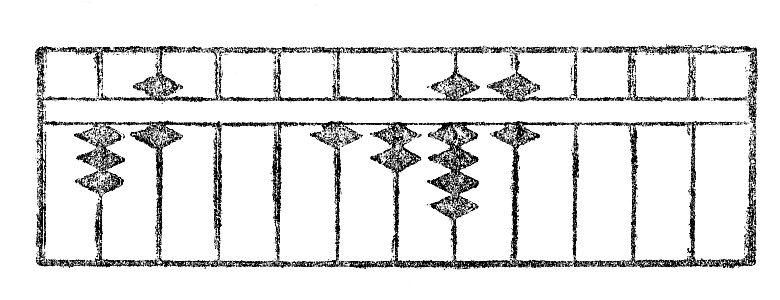
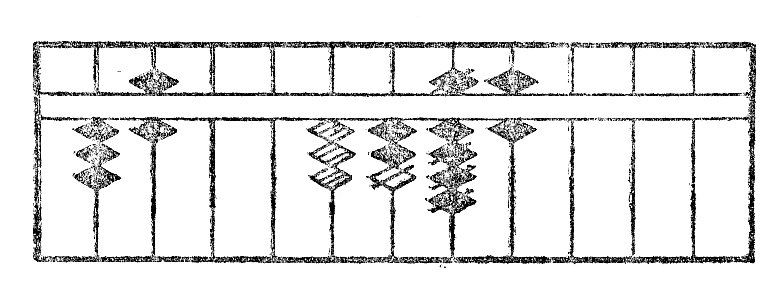
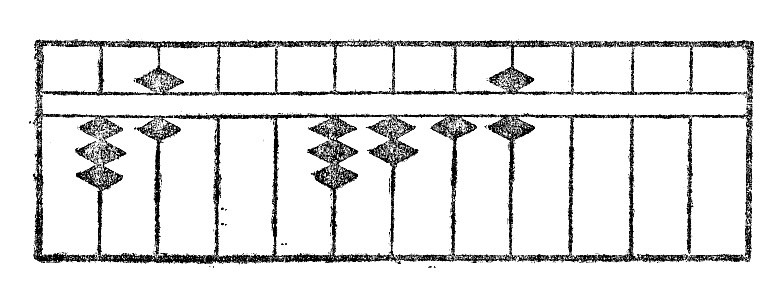
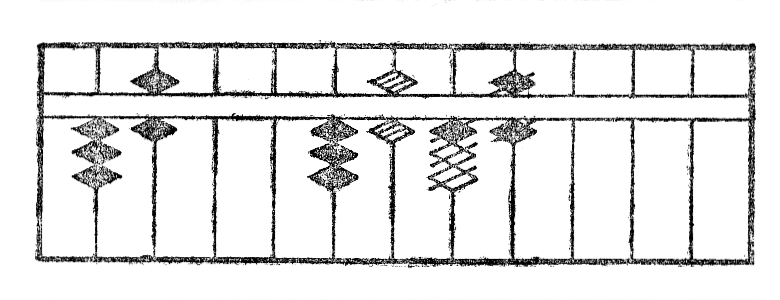
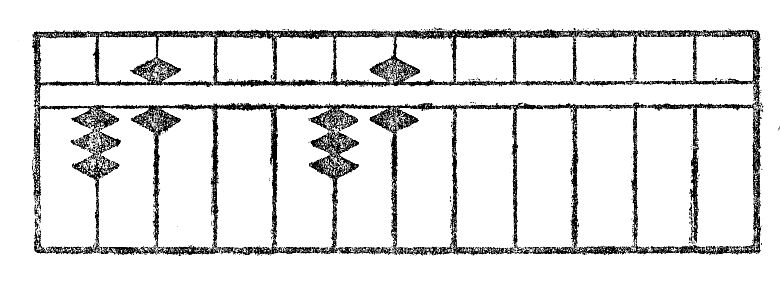
La figuro XIIIa montras la unuan aranĝon de kalkulo; la fig. XIIIb aliformigon de 1 en 3 kaj aldonon de 1 al la dua, kaj fine subtrahon*26 de 18, produto de 3 per 6. La fig. XIIIc la rezultaton post unua divido. La fig. XIIId la dividon de la dua cifero kaj la XIIIe la finan rezultaton. La kvociento videble estas 36.
Rimarko I.—Kiam la cifero, kiu tuj sekvas la partan kvocienton ĵus ricevitan, estas pli granda ol la unua cifero de dividanto, oni deprenas de ĝi certan nombron da fojoj nombron egalan je la unua cifero de dividanto kaj aldonas al la provizora kvociento tiom da unuo, kiom da fojoj tia subtraho*27 efektiviĝis. Se kontraŭe la sekvanta cifero estas tro malgranda, por ke la subtraho*28 povu efektiviĝi, oni malpliigas de unuo la provizoran kvocienton kaj aldonas al la sekvanta cifero nombron egalan je la unua cifero de dividanto; oni ripetas saman operacion, ĝis la subtraho*29 de parta produto fariĝas ebla.
Rimarko II.—Se la cifero dividota estas egala*30 je la unua cifero de dividanto, kaj plie se la nombro formita kune kun ĝi kaj sekvantaj ciferoj, kies nombro entute egalas la nombron da ciferoj en dividanto, estas pli malgranda ol la dividanto, oni aliformigas tiun ciferon dividotan en 9 kaj aldonas al ĝia dekstre apuda cifero nombron egalan je la unua cifero de dividanto.
Ekzemplo: Estu dividi 23688 per 24. La operacio estas montrita per la figuroj XIV.
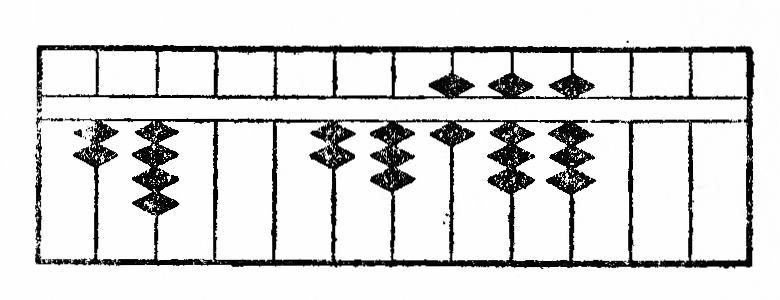
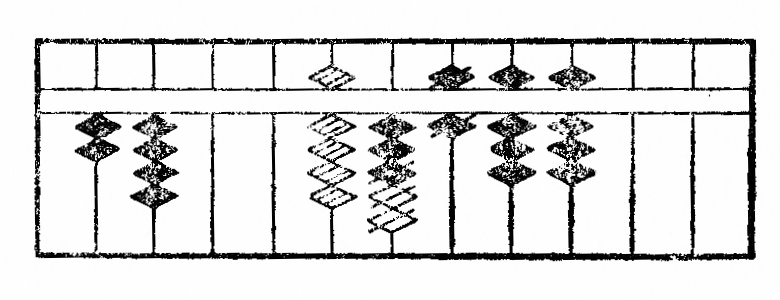
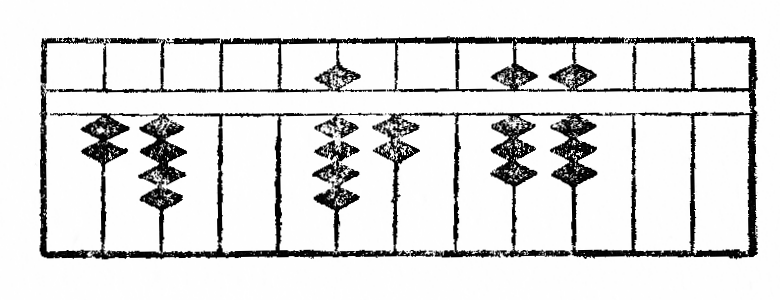
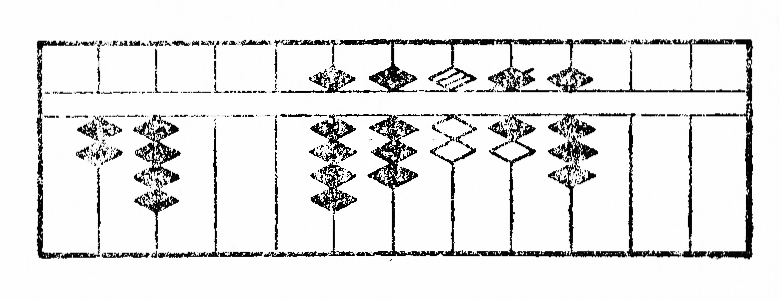
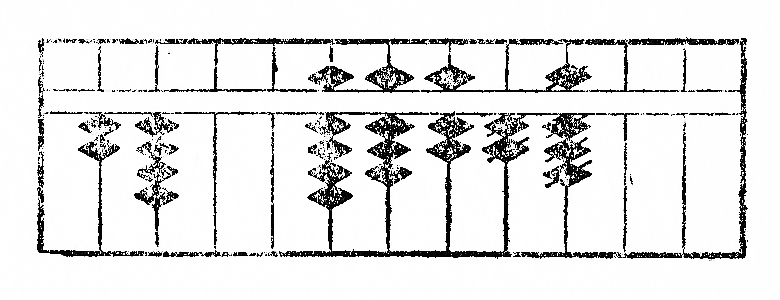
Ĉar la unue dividota cifero 2 estas egala je la unua de dividanto kaj plie 23 estas pli malgranda ol 24, mi aliformigas 2 en 9 kaj aldonas 2 al la sekvanta cifero 3, poste mi deprenas de 56 la produton de 9 per 4, kiel montras la figuro XIVb; post tiu ĉi subtraho*31 oni ricevas la figuron XIVc. Nun la nova cifero dividota 2 estante ankaŭ egala je la unua de dividanto kaj plie 20 plimalgranda ol 24, mi aliformigas 2 en 9 kaj aldonas 2 al la sekvanta cifero, sed ĉar mi ne povas depreni de la resto 28 la produton de 9 per 4, mi malpliigas de 1 la provizoran kvocienton kaj aldonas 2 al la sekvanta cifero, por ke la nombro 48, formita kun du sekvantaj ciferoj fariĝu pli granda ol la produto de 8 per 4. Post la subtraho*32, sekve post la dua divido la figuro fariĝas, kiel montrita per la fig. XIVf. Nun mi havas dividi la trian ciferon 1. Laŭ la regulo mi aliformigas ĝin en 5, sed ĉar la sekvanta cifero 6 estas pli granda ol la unua de dividanto kaj mi povas depreni de ĝi du fojojn nombron egalan je la unua cifero de dividanto, mi deprenas de ĝi 4 kaj pliigas de 2 la provizoran kvocienton, kiu tiel fariĝas 7. (fig. XIVg). Se mi nun subtrahas*33 de la kun ĝin sekvantaj du ciferoj formita nombro la produton de 7 per 4, mi ricevas nulon kiel resto, la divido estas do finita. La kvociento serĉita estas videble 987.
Sur kiu stangeto kuŝos la unuoj de la kvociento? Jen estas la regulo por ĝin trovi:
Regulo. —De la stangeto, kie kuŝas la unuoj de dividato, paŝu maldekstren tiom da stangetoj, kiom la dividanto enhavas da ciferoj en ĝia entjera parto, vi trovos tie la unuojn de kvociento. Se la dividanto ne havas entjeran parton, paŝu dekstren tiom da stangetoj kiom ĝi havas da nuloj post komo.
Ekzemple estu dividi 456,25 per 36,5. La unuoj de dividanto kaj dividato respektive kuŝante sur stangetoj M kaj N, la unuoj de kvociento sin trovas sur la stangeto R. Sur la figuro XVb oni vidas, ke la kvociento estas 12,5.
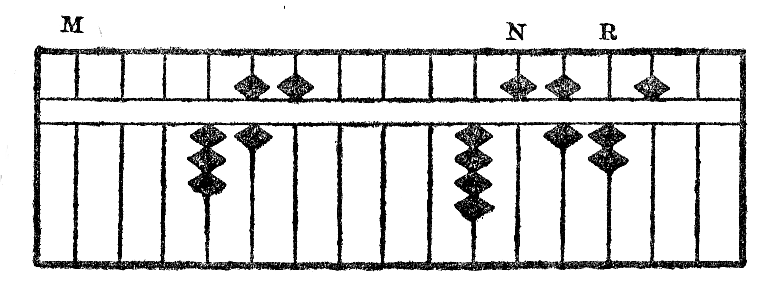
La divido de 45,625 per 0,00365 estas montrita per la figuroj XVI. La kvociento videble estas 12500.
Mi rimarkigas fine, ke la reguloj por trovi la lokon, kie devas sin trovi la unuoj de produto aŭ kvociento, permesas al ni, sen ia pripenso, plimallongigi la operacion por ricevi rezultaton kun dezirataj proksimumaj valoroj, kiam la nombroj konsideritaj enhavas en si tre multe da decimaloj.
La sorobano permesas al ni tre simple kaj tre rapide trovi radikon kvadratan, eĉ pli rapide ol per logaritmo.
Unue oni metas sur la ilo la nombron, kies radikon oni serĉas. De la stangeto, sur kiu sin trovas la unuoj de nombro konsiderita, paŝu maldekstren po du stangetoj, komputante : unuo, deko, cento, milo, k. t. p. ĝis ĉiuj ciferoj sin trovas tute en ĝia dekstra flanko, kaj metu tie, kie vi haltis, kiel eble plej grandan nombron, kies kvadrato sin trovas en la kun ĝin sekvantaj du ciferoj formita nombro. Se la nombro ne havas parton entjeran, paŝu dekstren po du stangetoj komputante: dekono, centono, milono, k. t. p. ĝis vi renkontas ciferon, kaj de tie vi revenu maldekstren du stangetojn kaj metu tien kiel eble plej grandan nombron, kies kvadrato povas esti enhavata en la kun ĝin sekvantaj du ciferoj formita nombro.
Oni deprenas la kvadraton de la nombro metita, t. e. unua cifero de radiko serĉita, de la kun ĝin sekvantaj du ciferoj formita nombro. Post tiu subtraho*34 oni dividas la tutan reston per 2.
Nun oni dividas la reston per la unua cifero de radiko jam ricevita; la kvociento ĵus ricevita donas la duan ciferon de radiko; oni deprenas ĝian duonkvadraton. Post tiu subtraho*35 oni dividas la reston per la nombro formita kun la du unuaj ciferoj de radiko kaj deprenas de la nova resto la duonkvadraton de la tria cifero ĵus ricevita, k. t. p. Oni tiel daŭrigas operacion, ĝis oni ricevis la radikon kun dezirataj proksimumaj valoroj. Kiam la kvociento estas tro granda, por ke oni povu subtrahi*36 ĝian duonkvadraton, kompreneble oni malpliigas de unuo, kiel oni vidis en divido.
Pri la subtraho*37 de duonkvadrato oni zorgu, ke ĝiaj unuoj sin trovu sur la stangeto, kies rango rilatante je la kvociento estas egala je tio de tiu ĉi lasta, rilatante je la unua cifero de radiko.
Ekzemple estu radikigi la nombron 42693156.
Mi unue metas la nombron sur la ilon, kiel montrita per la fig. XVIIa. Nun mi metas apud la unua cifero 4 la nombron 6, kiu estas la plej granda nombro, kies kvadrato estas enhavata en 42, nombro formita kun du sekvantaj ciferoj, kaj deprenas de tiu ĉi ĝian kvadraton; tio donas la figuron XVIIb.
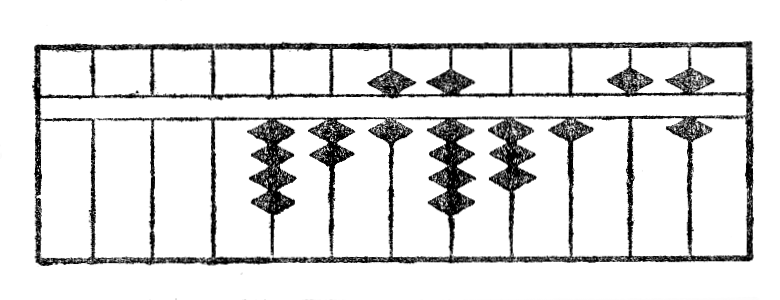
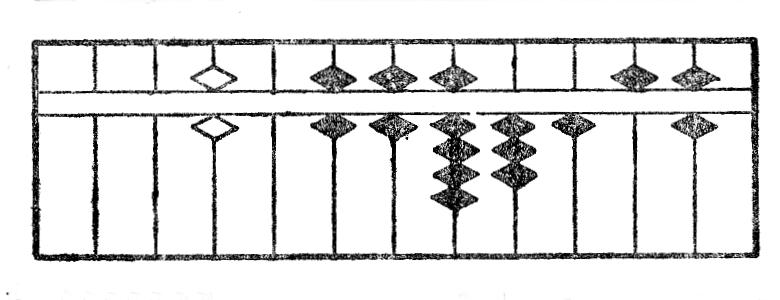
Post la divido de la resto per 2 la figuro fariĝas XVIIc. Nun dividante la reston per la unua cifero 6 mi ricevas 5 kiel kvocienton*38 kaj la rezultato post la subtraho*39 de ĝia duonkvadrato estas montrita per la figuro XVIId.
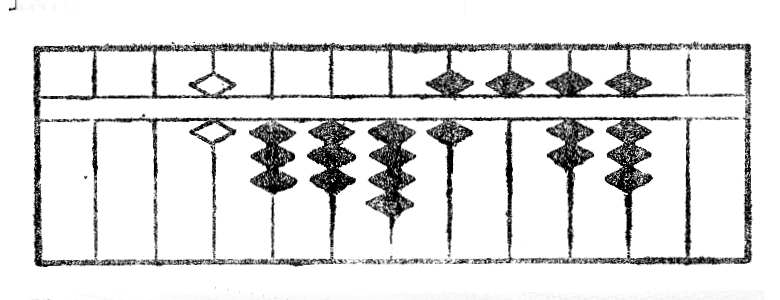
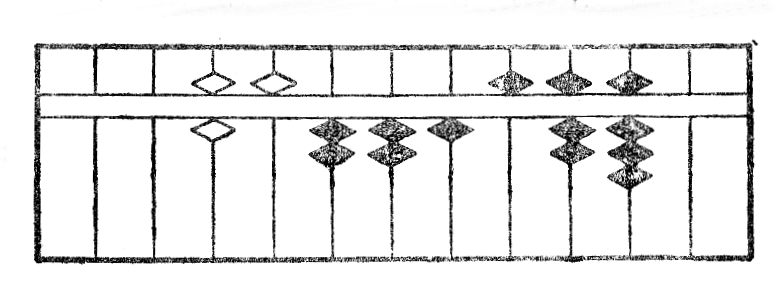
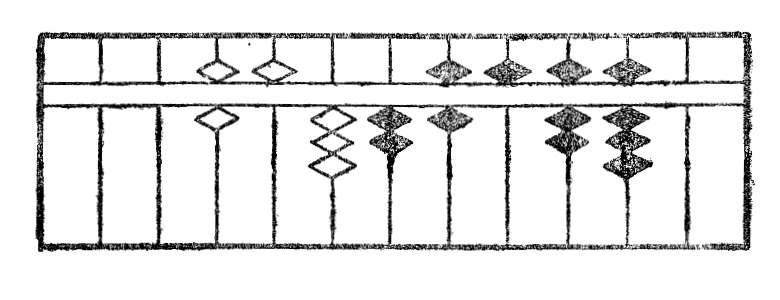
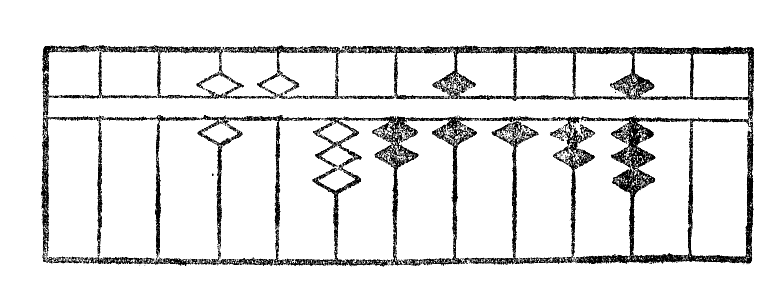
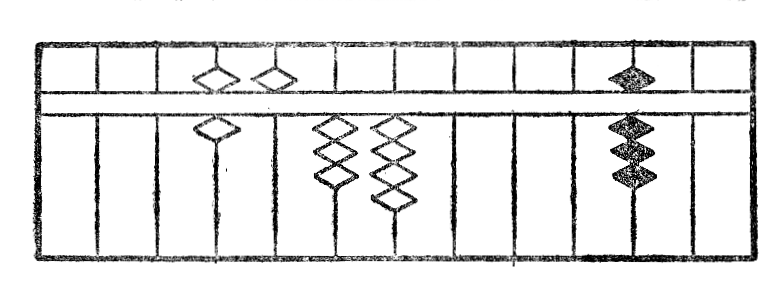
Denove dividante la reston per 65, nombro formita kun du unuaj ciferoj de radiko, mi ricevas 3 kiel kvocienton*40 (fig. XVIIe.) kaj la rezultato post la depreno de ĝia duonkvadrato estas montrita per la figuro XVIIf. La divido per tri unuaj ciferoj donas 4 kiel kvocienton*41 (fig. XVIIg), deprenante nun ĝian duonkvadraton mi ricevas nulon kiel resto kaj la operacio estas finita. La radiko serĉita estas videble 6534 (fig. XVIIh).
(5) La sorobano kostas Sm 2—3 laŭ la kvalito.
(6) Pli praktike estas, ke oni havas du globetojn suprajn sur ĉiu stangeto; oni ordinare uzas tian ilon.
(7) En ĉi tiu figuro kaj ĉiuj sekvantaj, pro la simpligo de figuro oni forlasis ĉiujn globetojn, kiuj ne estas necesaj.
AP=Antaŭparolo, Reg=Pri Registrilo de Pluvintenseco, Cik=Ciklonoj, kiuj ruinigis Formoson,
Rim=Rimarkindaj Ciklonoj Dar=Noto je la Tertremo en Dardanela Markolo,
Eks=Eksperimento pri Tertremado Kaŭzita de Veturanta Vagonaro, Soro=Pri Kalkulilo, Soroban'o
| VORTOJ | EN LA FONTO | LOKO | RIMARKOJ | |
| 1 | Meteorologia Observatorio | Meteorologia Observatrio | AP | |
| 2 | movi supren malsupren | movi supren malsuperen | Reg | |
| 3 | branĉo estas lutita | branĉo estas soldita | Reg | Arkaismo ne akceptita. |
| 4 | U-tubo | U tubo | Reg | |
| 5 | supozite konstanta | supozite konstata | Reg | |
| 6 | distanco de 120 km | distanco da 120 km | Cik | |
| 7 | kvanton de 964mm | kvanton da 964mm | Cik | |
| 8 | nombro de homoj | nombro da homoj | Rim | |
| 9 | nombron de domoj | nombron da domoj | Dar | |
| 10 | minimuman distancon | minumuman distancon | Eks | |
| 11 | perpendikle je la fervojo | perpendikale je la fervojo | Eks | |
| 12 | movis | movigis | Eks | |
| 13 | relative malrapida tremetado | rilative malrapida tremetado | Eks | |
| 14 | tuno | tono | Eks | |
| 15 | meteorologoj | meteorologistoj | Soro | |
| 16 | subtraho | subtraĥo | Soro | |
| 17 | la rezultato per si mem | la rezultato si mem | Soro | |
| 18 | Fig. II | Fig. III | Soro | |
| 19 | globeto supra | globeto supera | Soro | |
| 20 | subtrahon | subtraĥon | Soro | |
| 21 | subtrahi | subtraĥi | Soro | |
| 22 | montrita | montria | Soro | |
| 23 | subtrahon | subtraĥon | Soro | |
| 24 | subtrahoj | subtraĥoj | Soro | |
| 25 | subtrahojn | subtraĥojn | Soro | |
| 26 | subtrahon | subtraĥon | Soro | |
| 27 | subtraho | subtraĥo | Soro | |
| 28 | subtraho | subtraĥo | Soro | |
| 29 | subtraho | subtraĥo | Soro | |
| 30 | egala | egla | Soro | |
| 31 | subtraho | subtraĥo | Soro | |
| 32 | subtraho | subtraĥo | Soro | |
| 33 | subtrahas | subtraĥas | Soro | |
| 34 | subtraho | subtraĥo | Soro | |
| 35 | subtraho | subtraĥo | Soro | |
| 36 | subtrahi | subtraĥi | Soro | |
| 37 | subtraho | subtraĥo | Soro | |
| 38 | kiel kvocienton | kiel kvocento | Soro | |
| 39 | subtraho | subtraĥo | Soro | |
| 40 | kiel kvocienton | kiel kvociento | Soro | |
| 41 | kiel kvocienton | kiel kvociento | Soro |
KOLOFONO Tiu ĉi elektronika libro estas farita kaj prilaborita de volontuloj de Biblioteko Sakura – Projekto por Elektronika Biblioteko Esperanta. Fontolibro: "Verkoj de D-ro Nakamura", verk. Kijoo NAKAMURA, eld. Japana Esperanto-Instituto, 1932. Enkomputiligo: HIROTAKA Masaaki Retpaĝigo: HIROTAKA Masaaki, SIMIZU Yuko Revizio: HIROTAKA Masaaki, SIBAYAMA Zyun'iti Provlego: SIBAYAMA Zyun'iti Enretigo: 2007-11-29 Korekto: 2008-04-21 Ĉiuj rajtas reuzi tiun ĉi libron kun kondiĉo ne forigi ĉi tiun kolofonon.
Biblioteko Sakura – Projekto por Elektronika Biblioteko Esperanta さくら文庫・エスペラント電子図書館プロジェクト http://www.vastalto.com/pebe/ (retpoŝto: pebe<ĉe>googlegroups.com)